We have in LO.1 Math G10
First: the Concepts
Second: the References
Third: the Videos links
Fourth: Skills
Fifth: the materials as PPT., DOCX., and PDF
In the Drive from this link
Few Notes:
Trigonometry, the branch of mathematics concerned with specific functions of angles and their application to calculations. There are six functions of an angle commonly used in trigonometry. Their names and abbreviations are sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (csc). These six trigonometric functions in relation to a right triangle are displayed in the figure. For example, the triangle contains an angle A, and the ratio of the side opposite to A and the side opposite to the right angle (the hypotenuse) is called the sine of A, or sin A; the other trigonometry functions are defined similarly. These functions are properties of angle A independent of the size of the triangle, and calculated values were tabulated for many angles before computers made trigonometry tables obsolete. Trigonometric functions are used in obtaining unknown angles and distances from known or measured angles in geometric figures.
Trigonometry developed from a need to compute angles and distances in such fields as astronomy, mapmaking, surveying, and artillery range finding. Problems involving angles and distances in one plane are covered in plane trigonometry. Applications to similar problems in more than one plane of three-dimensional space are considered in spherical trigonometry.
History of trigonometry
Classical trigonometry
The word trigonometry comes from the Greek words trigonal (“triangle”) and metron (“to measure”). Until about the 16th century, trigonometry was chiefly concerned with computing the numerical values of the missing parts of a triangle (or any shape that can be dissected into triangles) when the values of other parts were given. For example, if the lengths of two sides of a triangle and the measure of the enclosed angle are known, the third side and the two remaining angles can be calculated. Such calculations distinguish trigonometry from geometry, which mainly investigates qualitative relations. Of course, this distinction is not always absolute: the Pythagorean theorem, for example, is a statement about the lengths of the three sides in a right triangle and is thus quantitative in nature. Still, in its original form, trigonometry was, by and large, an offspring of geometry; it was not until the 16th century that the two became separate branches of mathematics.
Ancient Egypt and the Mediterranean world
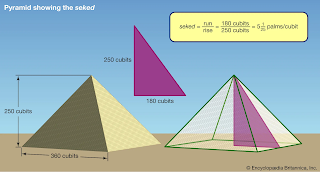
Several ancient civilizations—in particular, the Egyptian, Babylonian, Hindu, and Chinese—possessed considerable knowledge of practical geometry, including some concepts that were a prelude to trigonometry. The Rhind papyrus, an Egyptian collection of 84 problems in arithmetic, algebra, and geometry dating from about 1800 BCE, contains five problems dealing with the seked. A close analysis of the text, with its accompanying figures, reveals that this word means the slope of an incline—essential knowledge for huge construction projects such as the pyramids. For example, problem 56 asks: “If a pyramid is 250 cubits high and the side of its base is 360 cubits long, what is its seked?” The solution is given as 51/25 palms per cubit, and, since one cubit equals 7 palms, this fraction is equivalent to the pure ratio of 18/25. This is actually the “run-to-rise” ratio of the pyramid in question—in effect, the cotangent of the angle between the base and face. It shows that the Egyptians had at least some knowledge of the numerical relations in a triangle, a kind of “proto-trigonometry.”
We are glad for you to utilize our site. We furnish you with the assistance of introducing information to you as Egypt's extraordinary understudies in STEM Schools. This assistance is given from the data of master instructors and contemporary extraordinary understudies, and you can likewise help us in that by sharing your data, whatever it is through the WhatsApp and Telegram groups, which will You can discover them on the Home page of the site.💪Good Luck

 Posted by
Posted by 

comment 0 Comments
more_vert